TP2 - Les conditions

Objectifs

1. Comprendre le rôle d’une condition dans un programme ;
2. Utiliser les mots-clés if, elif et else ;
3. Tester des expressions logiques à l’aide des opérateurs de comparaison (<, >, ==, etc.) ;
4. Combiner plusieurs conditions avec and et or ;
5. Écrire un programme qui prend une décision en fonction des valeurs stockées dans des variables.

Au préalable

1. Se créer un dossier SNT sur votre ordinateur ou clé USB
2. Dans ce dossier, créer un dossier T3 - Programmation (Programmation Orientée Objet)

Sur EduPython ou autre instance python, faire :

1. Créer un nouveau fichier en cliquant sur l'icône 📄, ou en appuyant sur CTRL+N
2. Enregistrer le fichier sous le nom TP2_Conditions en cliquant sur l'icône 💾, ou en appuyant sur CTRL+S

TP

L'ensemble des exercices se fait sur le logiciel EduPython.

Certains programmes que l'on écrit nécessitent de pouvoir prendre une décision en fonction d'une situation.
Imaginons un programme qui affiche la mention obtenue au brevet. La logique à employer serait la suivante :

Si la note est supérieure à 16, alors il a mention très bien. 
Sinon, si elle est supérieure à 14, alors il a mention bien. 
Sinon, si elle est supérieure à 12, alors il a mention assez bien.

En programmation, ce type de décision s'appelle une structure conditionnelle.
Elles sont représentées, en français, par la structure suivante :

SI une condition est vraie :
    On exécute ces instructions
SINON SI une autre condition est vraie :
    On exécute plutôt ces instructions
SINON :
    on va exécuter celles-là

En python, on représente cette structure ainsi :

if condition1 :
  # instructions si la condition1 est vraie
elif condition2 :
  # instructions si la condition1 est fausse et que la condition2 est vraie
else :
  # instructions si aucune condition n'est vraie

• if signifie si
• elif signifie sinon si
• else signifie sinon
• condition représente un test à effectuer, très souvent de nature mathématiques, est écrit à l'aide des opérateurs suivants :

< (inférieur)

< : Strictement inférieur.

age = 12
if age < 18:
    print("Tarif réduit")

Si ce que contient la variable age est strictement inférieur à 18, alors on affiche "Tarif réduit".

<= (inférieur ou égal)

<= : Inférieur ou égal.

note = 10
if note <= 10:
    print("Résultat insuffisant ou juste la moyenne")

Si ce que contient la variable note est inférieur ou égal à 10, alors on affiche "Résultat insuffisant ou juste la moyenne".

> (supérieur)

> : Strictement supérieur.

score = 1200
if score > 1000:
    print("Niveau expert")

Si ce que contient la variable score est strictement supérieur à 1000, alors on affiche "Niveau expert".

>= (supérieur ou égal)

>= : Supérieur ou égal.

points = 50
if points >= 50:
    print("Bonus débloqué")

Si ce que contient la variable points est supérieur ou égal à 50, alors on affiche "Bonus débloqué".

== (égal)

== : Égal.

code = 1234
if code == 1234:
    print("Code correct")
else :
    print("Code incorrect")

Si ce que contient la variable code est égal à 1234, alors on affiche "Code correct". Sinon, on affiche "Code incorrect".

!= (différent)

!= : Différent.

couleur = "rouge"
if couleur != "bleu":
    print("Couleur incorrecte")

Si ce que contient la variable couleur est différent de "bleu", alors on affiche "Couleur incorrecte".

and (et)

and : Et.

moyenne = 15
serieux = True #Signifie "Vrai"
if moyenne > 14 and serieux == True :
    print("L'élève a les félicitations")

Si ce que contient la variable moyenne est supérieur à 14 et si ce que contient la variable serieux est égal à True, alors on affiche "L'élève a les félicitations".

or (OU)

or : Ou.

jour = "samedi"
if jour == "samedi" or jour == "dimanche":
    print("C’est le week-end")

Si ce que contient la variable jour est égal à "samedi" ou si ce que contient la variable jour est égal à "dimanche", alors on affiche "C’est le week-end".

Prise en main

1. Recopier puis exécuter le programme suivant :

   a = 5
   test = 6 * a + 2
   
   print("Le test vaut :", test)
   
   if test > 20:
       print("Condition vraie → test réussi")
   else:
       print("Condition fausse → test loupé")

   1. Quelle est la valeur calculée pour test ?
   2. La condition test > 20 est-elle vraie ou fausse ?
   3. Qu’est-ce que Python affiche ?
2. Modifier la valeur de a par 1. Exécuter à nouveau le programme.
   1. Quelle est la nouvelle valeur de test ?
   2. La condition devient-elle vraie ou fausse ?
   3. Le résultat affiché change-t-il ? Pourquoi ?
3. Tester avec d’autres valeurs de votre choix (par exemple 0, 10, 50).
   Trouver une valeur de a pour laquelle la condition devient vraie.

Cinéma

Le cinéma Excelsior de Saint-Dié propose plusieurs tarifs pour voir des films :

• 7 € pour les plus de 24 ans ;
• 5 € de 14 à 24 ans ;
• 4 € de 6 à 14 ans ;
• 3 € en dessous de 6 ans.

1. Créer une variable age contenant une valeur de votre choix.
   Afficher simplement son contenu avec print(age) pour vérifier que tout fonctionne.
2. Écrire maintenant un programme qui affiche uniquement le tarif de la première tranche, c’est-à-dire :
   • si l'âge est strictement supérieur à 24, afficher 7 euros.
3. Ajouter la deuxième tranche d’âge :
   • sinon si (elif) l'âge est supérieur ou égal à 14, afficher 5 euros. Tester votre programme avec plusieurs valeurs.
4. Compléter le programme avec les deux autres tranches :
   • de 6 à 14 ans → 4 euros
   • moins de 6 ans → 3 euros
5. Tester votre programme avec au moins 4 âges différents.
   Vérifier que le résultat correspond bien au tableau des tarifs.

Réciproque du théorème de Pythagore

La réciproque du théorème de Pythagore dit que :

Si a² + b² = c² alors le triangle est rectangle.

⚠️ En Python, on écrit un carré avec **2.
Exemple : a**2 signifie a².

1. Faire un programme qui permet de saisir 3 entiers a, b et c.

   Saisir des entiers

   Pour saisir une valeur entière, on utilise :

   entier = int(input("Saisir une valeur : "))

   input demande une saisie, et int convertit cette saisie en nombre entier.

2. Recopier et compléter dans votre programme le calcul suivant :

   somme = ... + ...
   carre_c = ...
   print(..., ...)

   Cela permet de vérifier visuellement les valeurs obtenues.

3. Ajouter ensuite une condition permettant de tester si le triangle est rectangle :

   • Si a² + b² est égal à c² → afficher "triangle rectangle"
   • Sinon → afficher "triangle non rectangle"

4. Tester votre programme avec plusieurs valeurs :

   • 3, 4, 5 → triangle rectangle
   • 2, 3, 4 → triangle non rectangle
   • Vos propres exemples

Triangle isocèle

On souhaite faire un programme qui permet de saisir 3 entiers a, b et c, correspondants aux valeurs des segments du schéma suivant :

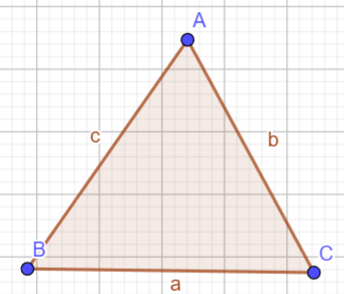
Le programme doit vérifier grâce aux entiers si le triangle est isocèle.

1. Faire un programme qui permet de saisir 3 entiers a, b et c.
2. Rajouter dans ce programme les conditions nécessaires pour vérifier grâce aux variables, si le triangle est isocèle, et afficher "isocèle" ou "non isocèle" en conséquence.
3. Modifier le programme pour vérifier si un triangle est équilatéral.

Points dans un repère

Dans un repère, un point (A) est représenté par son abscisse (X_A) et son ordonnée (Y_A).

On définit trois points :
A(4 ; 4), B(6 ; 4) et C(4 ; 4).

1. À l’aide de deux variables pour chaque point, stocker les coordonnées de chacun d’eux.
   On pourra utiliser : xa, ya, xb, yb, etc.
2. Deux points sont identiques s’ils ont la même abscisse et la même ordonnée.
   À l’aide d’une condition, vérifier et afficher "même coordonnées" si les points A et B sont identiques, ou "différentes coordonnées" sinon.
3. Tester le programme en comparant cette fois les points A et C, et observer le résultat.

La distance entre deux points est donnée par la formule :

$$\sqrt{(X_B - X_A)^2 + (Y_B - Y_A)^2}$$

4. Calculer les distances AB et BC, puis, à l’aide d’une condition, afficher "identique" si les deux distances sont égales, ou "non identique" sinon.