TD1 - Le rendu de monnaie
- Rappels des algorithmes gloutons ;
- Comprendre le concept de la programmation dynamique ;
- Mettre en place une solution dynamique ;
Le TD se fait sur papier.
Le rendu de monnaie est un problème d'optimisation cherchant à rendre une monnaie avec un nombre minimal de pièces, sur un système monétaire donné.
Rappels de Première : Les algorithmes gloutons
Un algorithme glouton est un algorithme prenant en compte à chaque fois la valeur la plus grande qu'il peut obtenir pour faire ses calculs, puis la seconde plus grande, et ainsi de suite, jusqu'à obtenir une solution finale (qui n'est pas forcément la meilleure).
On donne les pièces (en €) suivantes : 1, 2, 5, 10, 20, 50, 100, 200, disponibles en quantité illimitée dans le cadre de l'activité.
Voici un exemple de rendu de monnaie sur le montant 13€ avec un algorithme dit glouton :
La valeur la plus grande inférieure ou égale à 13€ est 10€.
On rend donc une pièce de 10€, il reste 3€.
La valeur la plus grande inférieure ou égale à 3€ est 2€.
On rend donc une pièce de 2€, il reste 1€.
La valeur la plus grande inférieure ou égale à 1€ est 1€.
On rend donc une pièce de 1€, il reste 0€. L'algorithme s'arrête.
On a donc rendu 3 pièces : 10€, 2€ et 1€.
- En reprenant l'exemple de l'algorithme glouton de l'énoncé, et le système monétaire (en €) suivant : 1, 2, 5, 10, 20, 50, 100, 200, calculer le nombre de pièces à rendre avec un montant de 28€.
- Nous ne disposons plus de pièces de 1€. Calculer le nombre de pièces à rendre avec un montant de 36€. Que se passe-t-il ?
L'algorithme glouton peut se retrouver bloqué car on ne peut pas retourner en arrière une fois qu'une pièce est rendue.
Il faut donc trouver une façon plus optimale de rendre la monnaie.
Arbres
Le but va maintenant être de déterminer toutes les possibilités pour rendre la monnaie. On ne va donc pas se limiter à une solution, on va en trouver plusieurs, et déterminer la meilleure.
Voici un exemple de rendu de monnaie sur le montant 5€ en cherchant toutes les possibilités :
- On peut rendre une pièce de 5€ (1 pièce au total) ;
- On peut rendre 2 pièces de 2€ et une pièce de 1€ (3 pièces au total) ;
- On peut rendre une pièces de 2€ et 3 pièces de 1€ (4 pièces au total) ;
- On peut rendre 5 pièces de 1€ (5 pièces au total).
On peut modéliser ce résultat sous la forme d'un arbre :
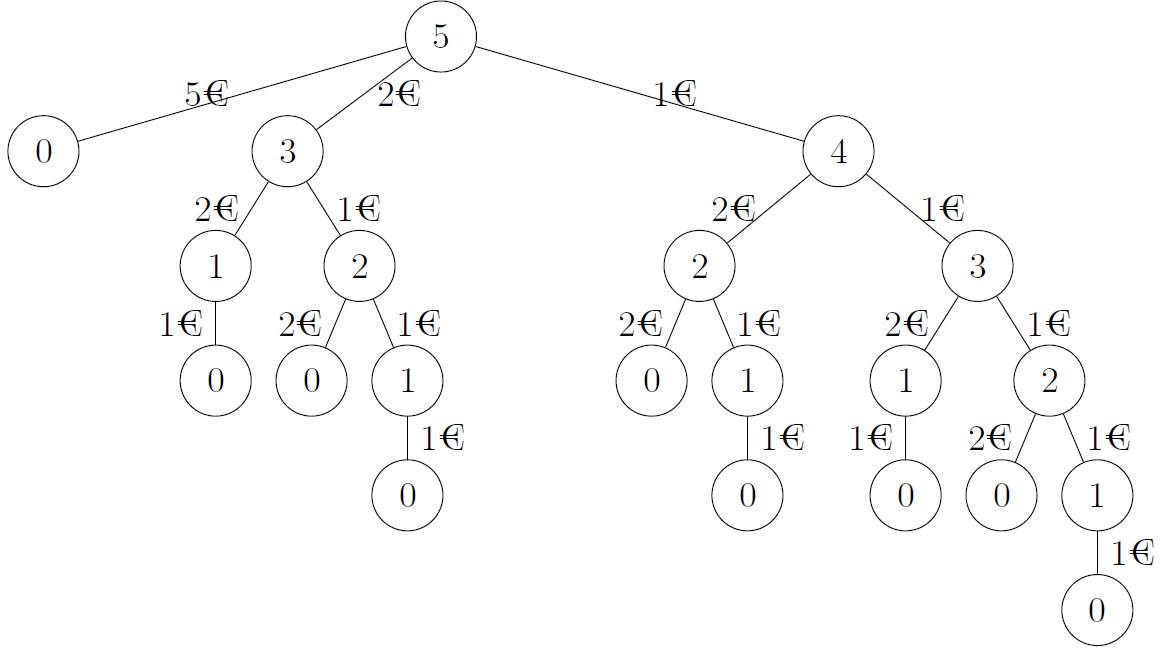
Les sommets représentent la somme restante, les arêtes la valeur de la pièce rendue.
- Sur cet arbre, combien de chemins existent-ils allant de la valeur 5 à la valeur 0 ?
- Quelle est la solution la plus optimale ? La moins optimale ?
- En déduire la façon de reconnaître les solutions les plus optimales.
On reprend le système monétaire (en €) suivant : 2, 5, 10, 20, 50, 100, 200 (nous n'avons plus de pièces de 1€).
- Écrire l'ensemble des solutions pour rendre 31€.
- Dessiner l'arbre correspondant au rendu des pièces.
Un algorithme glouton n'aurait pas pu nous donner de résultat pour rendre 31€, contrairement au traçage d'un arbre des possibilités.
Cependant, tracer ici des arbres peut être coûteux en temps, et en mémoire; on calcule plusieurs fois des valeurs qui ont déjà été calculées.
Mémoïsation��
On ne peut pas utiliser un algorithme glouton car cela peut ne pas nous donner de résultat, ou bien pas le meilleur.
La solution de la partie 2 est trop gourmande en ressource. Pour avoir un programme optimal, il faut donc mémoïser certaines valeurs pour éviter d'avoir à les recalculer.
- Dans l'arbre de l'exemple ci-dessus, quelles branches se répètent ?
- Comment faudrait-il modifier l'arbre pour qu'il soit plus optimal ?
On reprend le système monétaire (en €) suivant : 1,2,5,10,20,50,100,200.
- Compléter le tableau suivant en indiquant, pour chaque montant, le nombre de pièces minimum qu'il faudrait rendre :
Montant (€) 1 2 3 4 5 6 nombre pièces 1 - Comment pourrait-on déterminer le nombre de pièces à rendre pour un montant de 7€ ?
On donne ce programme récursif, permettant de calculer la solution de la partie 2:
liste_Piece = [1,2,5,10,20,50,100,200]
def rendu_monnaie_rec(montant):
if montant==0:
return 0
else:
mini = 1000 #On définit une valeur minimale pour comparer
for i in range(len(liste_Piece)): #Parcours de la liste des pièces
if liste_Piece[i] <= montant:
#On prend une pièce, et on rendre dans un des fils de l'arbre
#On le fait à chaque fois qu'une pièce peut ^etre donnée
nbPiece = 1 + rendu_monnaie_rec(montant-liste_Piece[i])
#A la fin d'une branche, si le nombre de pièces trouvées est plus petit
if nbPiece < mini:
mini = nbPiece #On remplace
return mini
- Expliquer son fonctionnement.
- Comment pourrait-on utiliser une mémoire pour sauvegarder des solutions ?
On se propose, pour résoudre le problème, de créer 2 fonctions. La fonction principale du rendu de monnaie va calculer les possibilités, et mettre à jour la mémoire. La seconde fonction va quant à elle initialiser la mémoire, et va créer une liste avec autant d'éléments que le montant à rendre.
On dispose ainsi des fonctions suivantes :
liste_pieces = [1,2,10,20,50,100,200]
def rendu_monnaie(pieces,montant):
'''
Initialise une liste "memoire" de 'montant' éléments, et retourne le nombre de pièces à rendre grâce à la fonction
@param : pieces (list) liste d'entiers correspondant aux pièces, montant (int) montant à rendre
@return : (int) nombre minimum de pièces à rendre sur le montant donné
'''
memoire = ...
return rendu_monnaie_dynamique(..., ..., ...)
def rendu_monnaie_dynamique(pieces,montant,memoire):
'''
Calcule le montant minimum de pièces à rendre sur un montant donné, en mémoïsant dans une mémoire le rendu de chaque montant inférieur
@param : pieces (list) liste d'entiers correspondant aux pièces, montant (int) montant à rendre, memoire (list) liste d'entiers contenant pour chaque élément le nombre de pièces minimum à rendre pour l'indice donné
@return : (int) nombre minimum de pièces à rendre sur le montant donné
'''
if ... :
return 0
elif ... > 0:
return ...
else:
mini = 1000
for i in range(len(...)):
if ... <= ... :
nombre_piece = 1 + ...
if nombre_piece < ... :
mini = nombre_piece
... = mini
return mini
- Compléter les fonctions, et les tester.
- Calculer le temps obtenu pour rendre 30€ avec chacune des fonctions, et expliquer les résultats obtenus.