TP1 - Création de graphes

Objectifs

1. Comprendre la structure des graphes ;
2. Manipuler des classes ;
3. Différencier des Graphes non orientés des orientés.

Pré-requis

Suivre le cours sur les graphes.

• Créer un dossier Graphes
• Créer un fichier Classes_Graphe

Documentation

Pour chaque fonction créée, ne pas oublier de la documenter.

Graphes orientés

Dans cette première partie, nous allons implémenter une classe permettant de manipuler des graphes orientés à l’aide d’une liste d’adjacence.

La liste d’adjacence sera représentée en Python par un dictionnaire :

• chaque clé représente un sommet ;
• la valeur associée est la liste des sommets accessibles depuis ce sommet.

Si on regarde le dictionnaire suivant :

d = {"A":["B", "D"], "B":["A", "C"], "C":["A"], "D":[]}

Cela représente le graphe orienté suivant :

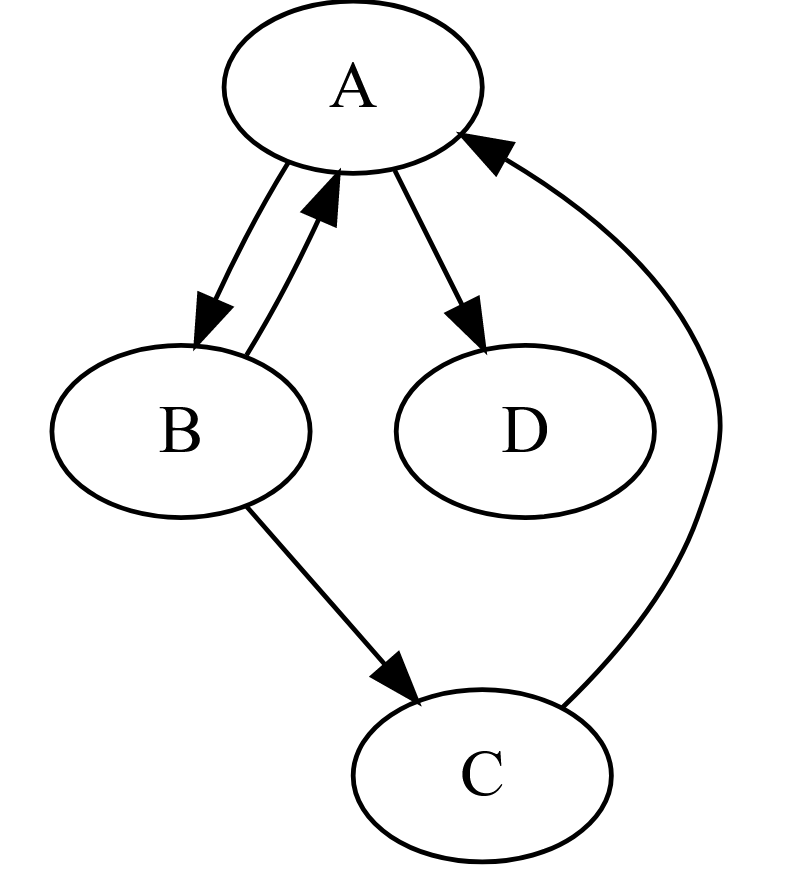
Création de la classe GrapheOriente

1. Créer une classe GrapheOriente.
2. Implémenter le constructeur __init__(self) qui initialise un attribut dico_adjacence à un dictionnaire vide.

---

Gestion des sommets

1. Implémenter la méthode ajouter_sommet(self, sommet) qui ajoute le sommet au graphe s’il n’existe pas déjà.
2. Implémenter la méthode sommets(self) qui retourne la liste des sommets du graphe, triée dans l’ordre croissant.
3. Implémenter la méthode contient_sommet(self, sommet) qui retourne True si le sommet est présent dans le graphe, False sinon.

Tests à effectuer

g = GrapheOriente()
g.ajouter_sommet("A")
g.ajouter_sommet("B")
g.ajouter_sommet("C")
print(g.sommets())
# ['A', 'B', 'C']
print(g.contient_sommet("B"))
# True
print(g.contient_sommet("D"))
# False

---

Gestion des arcs

Dans un graphe orienté, un arc relie un sommet de départ vers un sommet d’arrivée.

1. Implémenter la méthode ajouter_arc(self, sommet_1, sommet_2) qui :
   • ajoute les sommets au graphe s’ils n’existent pas ;
   • ajoute un arc orienté de sommet_1 vers sommet_2.
2. Implémenter la méthode arc_existe(self, sommet_1, sommet_2) qui retourne True si un arc de sommet_1 vers sommet_2 existe.

Tests à effectuer

g = GrapheOriente()
g.ajouter_arc("A", "B")
g.ajouter_arc("A", "C")
g.ajouter_arc("B", "C")
print(g.arc_existe("A", "B"))
# True
print(g.arc_existe("C", "A"))
# False

---

Voisins et degré

1. Implémenter la méthode voisins(self, sommet) qui retourne la liste des voisins accessibles depuis sommet, triée.
2. Implémenter la méthode degre(self, sommet) qui retourne le degré total du sommet (degré entrant + degré sortant).
   Rappel

   Dans un graphe orienté :

   • le degré sortant correspond au nombre d’arcs qui partent du sommet ;
   • le degré entrant correspond au nombre d’arcs qui arrivent sur le sommet.

Afficher le graphe

• Télécharger le fichier python afficheur_graphe à mettre dans le même dossier que le fichier Classes_Graphe ;
• Utiliser la fonction afficher_graphe(graphe), où graphe représente une instance d'un graphe.

Attention à nommer de la même façon la classe et les attributs.

Exercice

1. Recréer le graphe suivant :
   
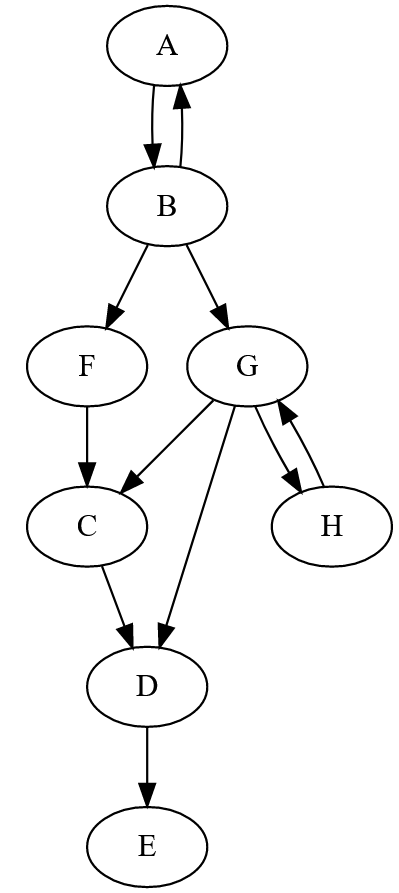
2. L'afficher.
3. Afficher les voisins de B.
4. Compter le degré de E.

---

Graphes non orientés

Dans cette seconde partie, nous allons implémenter une classe permettant de manipuler des graphes non orientés.

Dans un graphe non orienté, on parle d’arête : si un sommet A est relié à un sommet B, alors B est aussi relié à A.

La classe GrapheNonOriente héritera de la classe GrapheOriente.

Création de la classe GrapheNonOriente

1. Pour définir la classe GrapheNonOriente héritant de GrapheOriente, écrire la ligne suivante :

   class GrapheNonOriente(GrapheOriente):

Lorsqu’une classe hérite d'une autre classe, c’est comme si tout le code de la première classe était copié dans la nouvelle.
Le terme "redéfinir" signifie "récrire" le code d’une méthode dans la nouvelle classe pour l’adapter à un comportement voulu. Il suffit donc de récrire la fonction correspondante.

---

Gestion des arêtes

1. Redéfinir la méthode ajouter_arc(self, sommet_1, sommet_2) afin que :
   • sommet_2 soit ajouté aux voisins de sommet_1 ;
   • sommet_1 soit ajouté aux voisins de sommet_2.

Tests à effectuer

g = GrapheNonOriente()
g.ajouter_arc("A", "B")
g.ajouter_arc("A", "C")
print(g.arc_existe("A", "B"))
# True
print(g.arc_existe("B", "A"))
# True

---

Degré d’un sommet dans un graphe non orienté

1. Redéfinir la méthode degre(self, sommet) pour qu’elle retourne le nombre de voisins du sommet.
2. Tester la méthode sur plusieurs sommets.

Exercice

1. Recréer le graphe suivant :
   
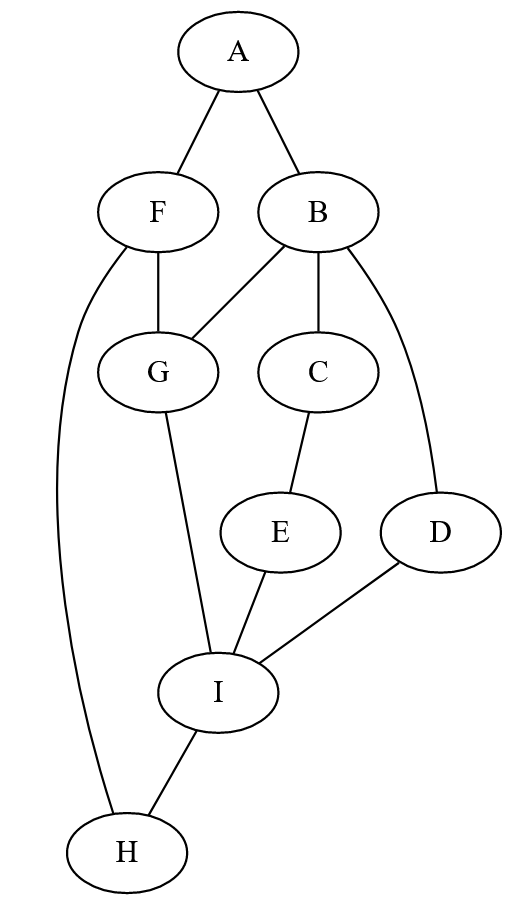
2. L'afficher.
3. Afficher les voisins de G.
4. Compter le degré de I.

Pour réfléchir davantage

Faire une méthode :

• supprimerArc(self, sommet1,sommet2) permettant la suppression de l'arc allant de sommet1 vers sommet2 ;
• supprimer_sommet(self, sommet) permettant de supprimer un sommet du graphe. Le sommet doit être supprimé :
  • de la liste des sommets ;
  • de toutes les listes de voisins des autres sommets.
• nombre_arcs(self) qui retourne le nombre total d’arcs du graphe.