Les graphes
En informatique et en mathématiques, un graphe est une structure de données qui modélise un ensemble d'éléments appelés sommets (ou nœuds) reliés par des arêtes (ou arcs).
Un graphe permet de représenter les relations entre objets ou entités.
Utilisations
Les graphes sont utilisés dans de nombreux domaines :
- Réseaux sociaux : utilisateurs ↔ connexions
- Routage et navigation : villes ↔ routes
- Réseaux informatiques : appareils ↔ connexions
- Biologie : interactions entre protéines ou gènes
- Planification : tâches avec dépendances (diagrammes de Gantt)
- Recherche sur le Web : pages web ↔ liens hypertexte
Types de graphes
Graphes non orientés (GNO)
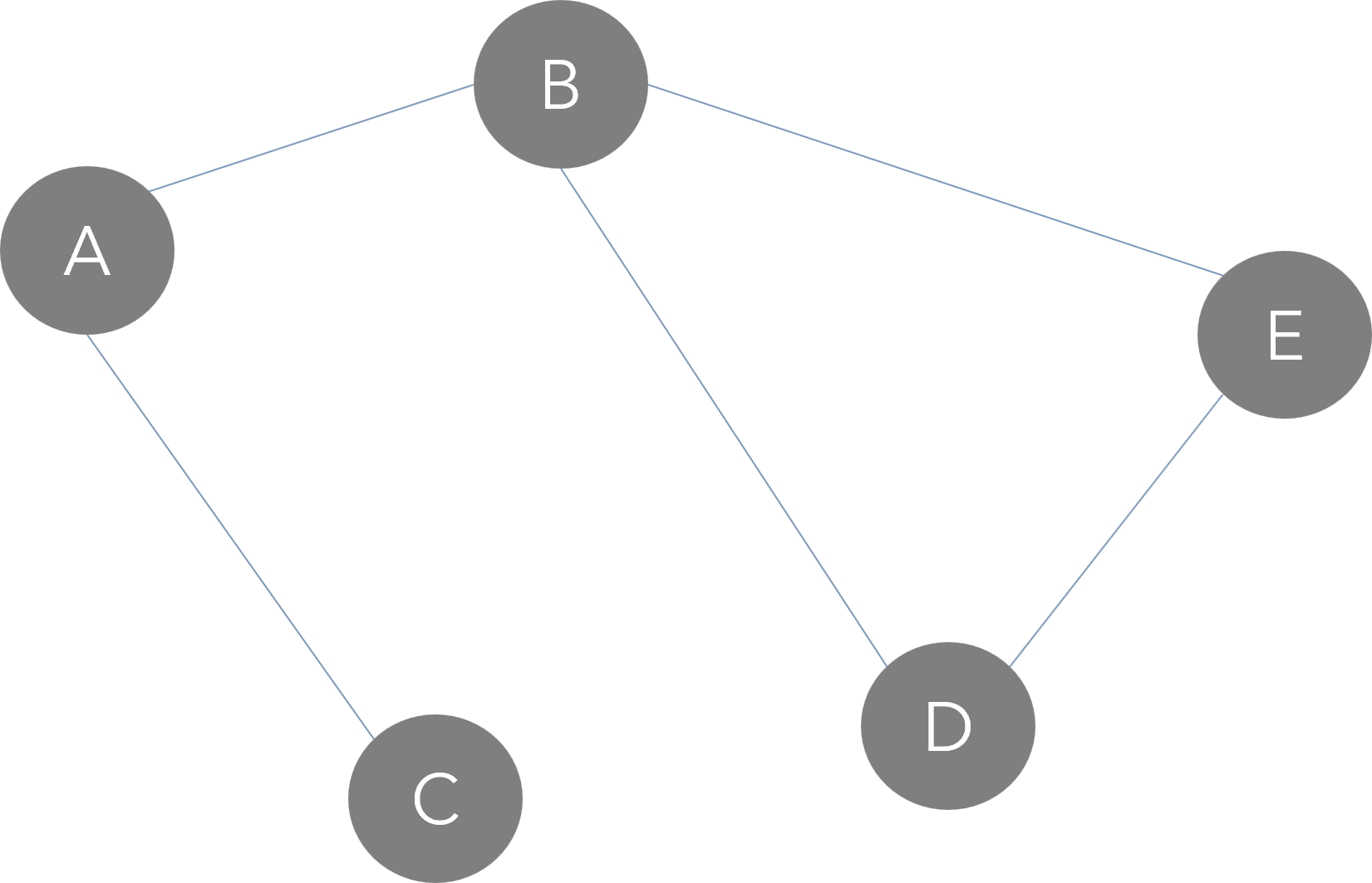
- Arêtes sans orientation : la relation est bidirectionnelle.
- Exemple : une route entre deux villes permet d’aller dans les deux sens.
Graphes orientés (GO)
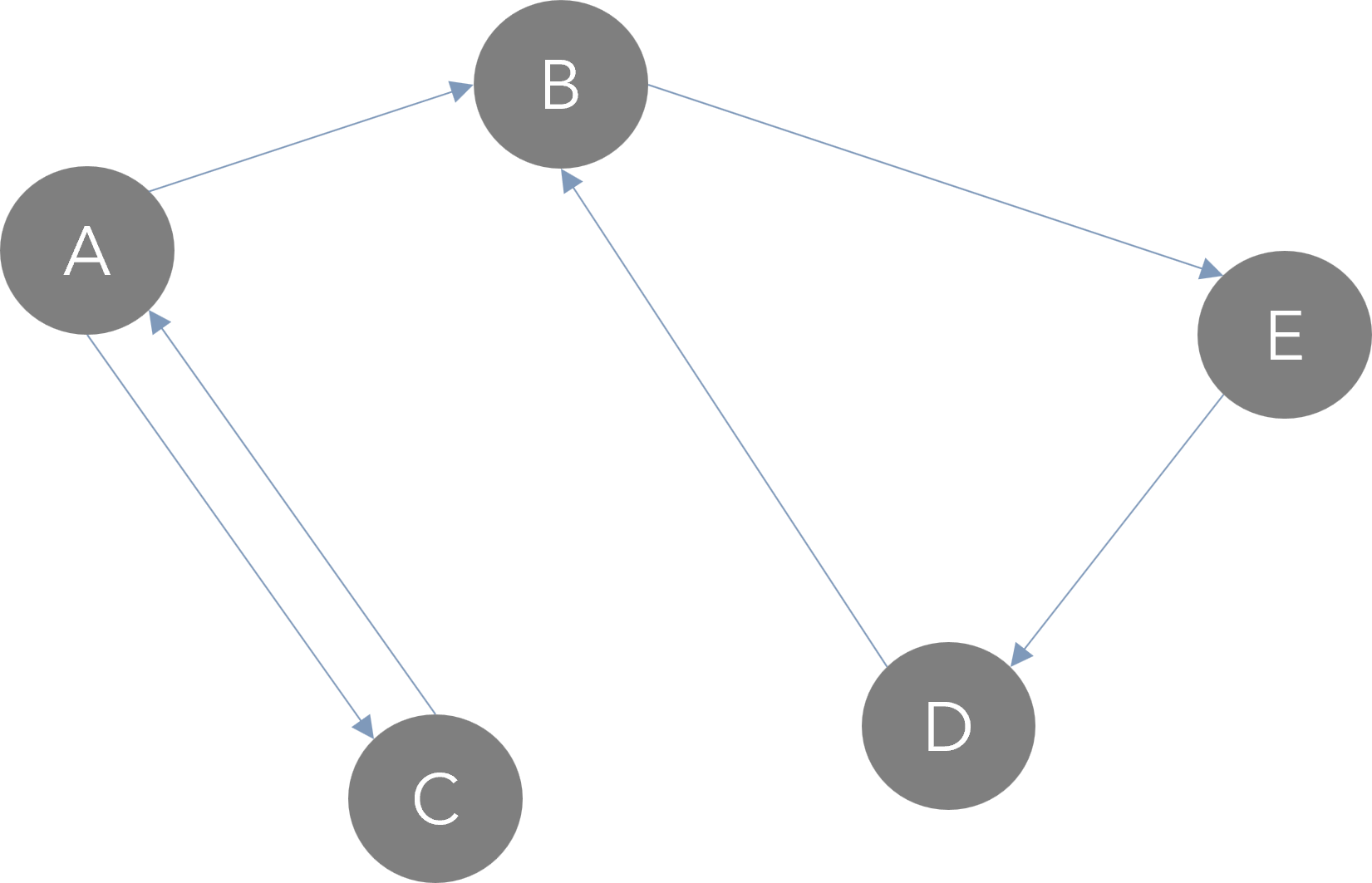
- Arcs avec orientation : la relation va dans un seul sens.
- Exemple : un sens unique de circulation, ou un lien hypertexte entre pages.
Propriétés des graphes
- Chemin / chaîne
- Cycle
- Degré
- Connexité
- Graphe pondéré
- Graphe acyclique
Un chemin (GO) ou une chaîne (GNO) est une séquence de sommets reliés par des arêtes/arcs allant d’un sommet de départ à un sommet d’arrivée.
Exemple (GNO) : pour aller de C à E : C - A - B - E.
Un cycle est un chemin ou une chaîne dont le sommet de départ est également le sommet d’arrivée.
Exemple (GNO) : B - E - D.
Le degré d’un sommet correspond au nombre de liens qu’il possède.
Notation : d(S) pour le degré d’un sommet S.
Exemple : d(A) = 2, d(C) = 1.
Notation :
d+(S): degré entrantd-(S): degré sortantd(S) = d+(S) + d-(S)
Exemple : d+(A) = 1, d-(A) = 2, d(A) = 3.
- Un GNO est connexe si tout sommet est accessible depuis tout autre sommet.
- Un GO est fortement connexe si chaque sommet est accessible depuis tout autre sommet via un chemin dirigé.
Un graphe pondéré attribue un poids à chaque arête ou arc (ex : distance, coût, temps).
La représentation matricielle contient alors les valeurs des poids au lieu de 0/1.
Un graphe acyclique ne contient aucun cycle.
Un DAG (Directed Acyclic Graph) est un graphe orienté acyclique, utile pour la planification de tâches.
Représentations des graphes
Matrices d’adjacence
Une matrice est un tableau contenant des entiers, représenté par cette notation :
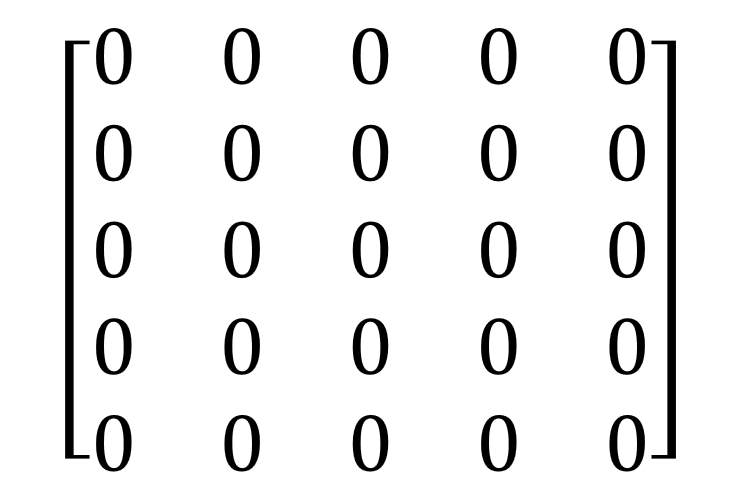
En Théorie des Graphes, cette notation peut être utilisée pour représenter simplement un graphe.
On utilise une matrice carrée (autant de colonne que de rangée) correspondant aux sommets.
L'objectif est de noter 1 dans la case où un sommet A est en lien avec un sommet B, 0 dans le cas contraire.
Cela s'applique autant pour un GO qu'un GNO.
Exemple de matrice avec le GO de la partie précédente :

Dans un GNO, la matrice d'adjacence est symétrique.
Listes d’adjacence
Pour chaque sommet, on liste les voisins (GNO) ou les successeurs/prédécesseurs (GO).
Exemple avec les graphes du cours :- GNO
- GO
| Sommet | Voisins |
|---|---|
| A | B, C |
| B | A, D, E |
| C | A |
| D | B, E |
| E | B, D |
| Sommet | Prédécesseurs | Successeurs |
|---|---|---|
| A | C | B, C |
| B | A, D | E |
| C | A | A |
| D | E | B |
| E | B | D |